Yasal Uyarılar’ 
Telif Hakkı ‘UYAR VE KALDIR’
Leonardo Fibonacci İtalya’nın Pisa şehrinde doğmuş olan İtalyan bir matematikçidir, bu nedenle Pisalı Leonardo olarak da anılmaktadır. Fibonacci bir problemi araştırırken bu sayıları buluyor ve kendi adını veriyor.
Leanardo Fibonacci??
Leonardo Fibonacci, (Pisalı Leonardo, Leonardo Pisano d. 1170, ö. 1250), yaygın olarak ismiyle Fibonacci diye anılan, orta çağın en yetenekli matematikçisi olarak kabul edilen İtalyan matematikçi
Fibonacci modern çağda en fazla Hint-Arap Sayılarını Avrupa'ya getirmesiyle ve 13. yüzyıl başlarında yayınlanan Liber Abaci isimli hesaplama yöntemleri kitabıyla tanınır. Liber Abaci'de bir örnek olarak yer alan modern sayılarla hesaplanmış kendi adıyla anılan sayı dizisi Fibonacci Dizisi olarak anılmaktadır. Sadece Fibonacci dizisi ve özellikleri ile ilgili kitaplar hatta haftalık düzenli yayınlanan matematik dergileri bile bulunmaktadır.
Biyografisi:
Leonardo 1170 yılında İtalya'nın Pisa şehrinde doğdu. Kesin doğum tarihi bilinmemektedir. Babası Guglielmo'dur.Takma adı Bonaccio idi ve bu ad, iyi tabiatlı veya sade ruhlu anlamına gelmekteydi. Annesi Alessandra,Leonardo 9 yaşındayken öldü. Leonardo babasının takma adını miras olarak aldı. İtalyanca Filius Bonacci, Bonacci'nin oğlu anlamına gelmekteydi ve Leonardo bu nedenle Fibonacci diye anılmaya başlandı.
Babası Guglielmo Cezayir'in Béjaïa limanı ile İtalya'nın Bugia kenti arasında bir ticaret postasını idare etmekteydi. Genç bir çocuk olan Leonardo babasına yardım etmek için onunla seyahat ederdi. Burası Leonardo'nun Hint-Arap sayı sistemini öğrendiği yerdir.
Fibonacci Hint-Arap sayıları ile aritmetik işlemler yapmanın Roma rakamları ile hesap yapmaktan çok daha basit ve verimli olduğunu gördü. Leonardo bütün Akdeniz bölgesini gezdi ve dönemin önde gelen Arap matematikçiler ile çalışma olanağı buldu. Leonardo yaklaşık olarak 1200 yıllarında bu seyahatinden döndü. 1202 yılına gelindiğinde 32 yaşında, öğrendiklerini "abaküs kitabı" veya "hesaplama kitabı" anlamına gelen Liber Abaci isimli eserinde topladı. Yayınladığı bu eserinde Hint-Arap Sayı Sistemi'ni Avrupa'ya duyurdu.
Leonardo matematik ve bilim ile ilgilenmeyi seven Roma İmparatoru II. Frederick ile dost oldu. 1240 senesinde Pisa cumhuriyeti kendisini Leonardo Bigollo namıyla taltif edip onurlandı ve maaş bağlandı.[4] 19. yüzyılda Pisa'da Fibonacci heykeli yapılmış ve buraya dikilmiştir. Heykel bugün Camposanto'nun batı galerisinde ve Piazza dei Miracoli tarihi mezarlığında bulunmaktadır.
Liber Abaci:
Liber Abaci'de (1202) Fibonacci, modus indium (Hintlerin Yöntemi) adını verdiği ve günümüzde Arap-Hint sayıları diye bilinen modern ondalık sayı sistemini tanıtır. Bu kitap gündelik hayatta ticari defter tutma, ölçü birimlerini çevirme, faiz hesaplama, para bozma ve değiştirme ve benzeri işlemlerde önemini göstermiştir. Kitap Avrupa'da tahsilli insanlar arasında hızlı bir şekilde yayılmış ve Avrupa'nın müspet bilimde ilerlemesine önemli etkileri olmuştur.
Liber Abaci'de ayrıca kapalı bir ortamdaki bir tavşan ailesinin artışını, her tavşan çiftinin bir ay sonra bir yavru yapıp onun da 1 ay sonra 1 yavru yapacağı gibi ideal varsayımlar altında hesaplanmasını gösterir. Bu problemin çözümünde tavşan çiftlerinin sayısının artışını gösteren sayı dizisi Fibonacci sayıları, diziye de Fibonacci dizisi denir. Bu sayı dizisi 6. yüzyıldan beridir Hint matematikçiler tarafından bilinmekteydi ancak Avrupa'ya ilk olarak Fibonacci tarafından tanıtılmıştır.
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987.. dizisi Fibonacci dizisi olarak geçiyor. Fibonacci dizisinin özelliği kendinden önceki iki ardışık sayının toplamının kenisinden sonraki sayıya eşit olmasıdır.
Dizilim içinde bir sayıyı kendisinden önce gelen sayıya bölerek ilerlersek ulaşacağımız sonuç 1,618 rakamına sürekli yaklaşacak şekilde oluşacaktır.
Tavşan Problemi
"Dört yanı duvarlarla çevrili bir yere bir çift tavşan konmuştur. Her çift tavşanın bir ay içinde yeni bir çift tavşan yavruladığı, her yeni çiftin de erginleşmesi için bir ay gerektiği ve tavşanların ölmediği varsayılırsa, 100 ay sonunda dört duvarın arasında kaç çift tavşan olur?" Bu şekilde düşünüldüğü takdirde tavşan çiftleri aylara göre şu sıralamayı ortaya koymaktadır: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89,
Fibonacci sayı dizisinin bu kadar popüler olmasının en önemli nedenleri doğada çokça rastlanması ve dizinin terimlerini kendinden sonraki terime bölünmesi sonucu elde edilen oranların giderek Altın Oran'a yaklaşması.
Fibonacci Sayı Dizisi nerelerde kullanılır?
Fibonacci Sayı Dizisinin Görüldüğü ve Kullanıldığı Yerler:
1) Ayçiçeği: Ayçiçeği'nin merkezinden dışarıya doğru sağdan sola ve soldan sağa doğru taneler sayıldığında çıkan sayılar Fibonacci Dizisinin ardışık terimleridir.
2) Papatya Çiçeği: Papatya Çiçeğinde de ayçiçeğinde olduğu gibi bir Fibonacci Dizisi mevcuttur.
3) Fibonacci Dizisinin Fark Dizisi: Fibonacci Dizisindeki ardışık terimlerin farkıyla oluşan dizi de Fibonacci Dizisidir.
4) Ömer Hayyam veya Pascal veya Binom Üçgeni: Ömer Hayyam üçgenindeki tüm katsayılar veya terimler yazılıp çapraz toplamları alındığında Fibonacci Dizisi ortaya çıkar.
5) Tavşan: Zaten sorumuz tavşanla alakalı…
6) Çam Kozalağı: Çam kozalağındaki taneler kozalağın altındaki sabit bir noktadan kozalağın tepesindeki başka bir sabit noktaya doğru spiraller (eğriler) oluşturarak çıkarlar. İşte bu taneler soldan sağa ve sağdan sola sayıldığında çıkan sayılar, Fibonacci Dizisi'nin ardışık terimleridir.
7) Tütün Bitkisi: Tütün Bitkisinin yapraklarının dizilişinde bir Fibonacci Dizisi söz konusudur; yani yaprakların diziliminde bu dizi mevcuttur. Bundan dolayı tütün bitkisi Güneş'ten en iyi şekilde güneş ışığı ve havadan en iyi şekilde Karbondioksit alarak Fotosentez'i mükemmel bir şekilde gerçekleştirir.
8 ) Eğrelti Otu: Tütün Bitkisindeki aynı özellik Eğrelti Otu'nda da vardır.
9) MİMAR SİNAN: Mimar Sinan'ın da bir çok eserinde Fibonacci Dizisi görülmektedir. Mesela Süleymaniye ve Selimiye Camileri'nin minarelerinde bu dizi mevcuttur.
Fibonacci Sayı Dizisi ve Altın Oran arasındaki ilişki
Fibonacci Sayıları ile Altın Oran arasında ilginç bir iliski vardir. Fibonacci sayı dizideki ardışık iki sayının bir birine bölünmesiyle elde edilen oran, sayılar büyüdükçe Altın Oran'a yaklaşır. Dizi ilerledikçe iki terim'in arasındaki oran 1,618′e yaklaşır.
Güneş etrafındaki gezegenlerin yörüngelerinin eliptik yapısını keşfeden Johannes Kepler (1571-1630), Altın Oran'ı şu şekilde belirtmiştir: "Geometrinin iki büyük hazinesi vardır; biri Pythagoras'ın teoremi, diğeri, bir doğrunun Altın Oran'a göre bölünmesidir." Bu oranı resmen kullandığı bilinen ilk kişi Parthenon'un mimarı Phidias'tır.
Şimdi sizinle altın oranın hakim olduğu başka fotoğraflar paylaşacağım. Eminim ki siz de benim gibi altın oranın kattığı estetiğe hayran kalacaksınız.
Şimdi sizinle altın oranın hakim olduğu başka fotoğraflar paylaşacağım. Eminim ki siz de benim gibi altın oranın kattığı estetiğe hayran kalacaksınız.
Peki nedir Fibonacci Sayılarını yüzyıllardır bu kadar önemli yapan?
1. Altın oran sayısının çok önemli bir sayı olması,
2. Dizinin daha küçük elemanlarının doğada karşımıza çıkması,
3. Sayıların sayılar teorisinde farklı birçok kullanımı olması Fibonacci sayılarını oldukça önemli yapmıştır.
.jpg)
Altın Oran
Fibonacci'nin kendi ismiyle bilinen sayı dizisi 1,1,2,5,8,13,21,34,55,... şeklindedir. Fibonacci sayı dizisindeki terimler kendinden önceki iki terimin toplanması ile elde edilmektedir. Ayrıca sayı dizisindeki ardışık iki terimin birbirine oranlanması ile elde edilen sayı sabittir. Bu sabit Fibonacci'nin ilk iki harfi olan Fi sayısı olarak adlandırılmıştır.
Ayrıca bu sabit oran Altın Oran olarak da bilinmektedir. Altın Oran, mimariden sanata, doğada bitkilerden insan vücuduna, kasırgalardan galaksilere kadar birçok yerde karşımıza çıkmaktadır. Bu yüzden yüzyıllardır insanların ilgisini çekmekte ve üzerinde çeşitli çalışmalar yürütülmektedir.
Fibonacci'nin kendi ismiyle bilinen sayı dizisi 1,1,2,5,8,13,21,34,55,... şeklindedir. Fibonacci sayı dizisindeki terimler kendinden önceki iki terimin toplanması ile elde edilmektedir. Ayrıca sayı dizisindeki ardışık iki terimin birbirine oranlanması ile elde edilen sayı sabittir. Bu sabit Fibonacci'nin ilk iki harfi olan Fi sayısı olarak adlandırılmıştır.
Ayrıca bu sabit oran Altın Oran olarak da bilinmektedir. Altın Oran, mimariden sanata, doğada bitkilerden insan vücuduna, kasırgalardan galaksilere kadar birçok yerde karşımıza çıkmaktadır. Bu yüzden yüzyıllardır insanların ilgisini çekmekte ve üzerinde çeşitli çalışmalar yürütülmektedir.
Altın Oran Nerede?
 | Deniz Kabuğu: Dipten başlayarak uca doğru ilerleyen kıvrımları bulunan deniz kabuğunun, logaritmik spiral denilen her birkıvrımına oluşan eğikliğin tanjantı altın orana denk gelmektedir. |
 | El Parmakları: Parmaklarımızın tam orta kısmındaki boğumu, altın oran doğrusundaki B noktası olarak kabul edersek; elimize doğru olan kısa parçanın tırnağımıza doğru olan uzun parçaya oranı ile tırnağa doğru olan uzun parçanın tüm parmağımıza olan oranı eşit olacaktır. Ayrıca büyük parçaların küçük parçalara oranı 1,618′i (Φ) verecektir. |
 | Kollar: Kolumuz dirseğimizden iki parçaya ayrılmaktadır. Kolumuzda omzumuza doğru olan kısa parçanın elimize doğru olan uzun parçaya oranı ile elimize doğru olan uzun parçanın tüm kolumuzun uzunluğuna oranı eşittir. Ayrıca büyük parçaların küçük parçalara oranı 1,618′i (Φ) vermektedir. |
 | Çam Kozalağı: Kozalağın içindeki merkez noktadan dışarıya doğru spiral biçiminde uzayan her bir tanenin eğrilik açısı, bizealtın oranı vermektedir. |
 | Salyangoz: Salyangozların sırtlarındaki sarmal kıvrımlar, onların korunarak büyümeleri için en uygun yöntemdir. Bu sarmal kıvrımlar bir kağıda aktarıldığında bir altın dikdörtgen elde edilmektedir. Yani bunun kısa kenarının uzun kenarına oranı altın orana eşittir. |
 | Saçtaki Düğüm Noktası: Her insanın kafasının tepe noktasında, saçların çıkmaya başladığı kıvrımlı bir düğüm noktası vardır. Resimde örneklendiği gibi bazı insanlarda bu iki tanedir. Bu düğüm noktasından çıkan saçların yaptığı kıvrım, bir açıyla ilerlemektedir. İşte bu eğimin tanjantı, bize altın oranı vermektedir. |
 | Tütün: Tütün ve eğrelti otu gibi bazı bitkilerin yaprakları, aşağıya doğru eğimli olarak uzamaktadır. Bu eğimin tanjant değeri altın oranı vermektedir. |
 | Selimiye Camisi: Mimar Sinan, altın oranı Edirne’deki Selimiye Camisi’nde kullanmıştır. Caminin minarelerindeki ışıklı bölmelerin oranı, altın oranına eşittir. Bu durum Süleymaniye Camisi’nde de geçerlidir. |
 | İnsan Yüzü: Yüzümüzde altın oranı bulabileceğimiz bir çok yer vardır. Bunlardan biri kaşların arasındaki boşlukla, gözbebekleri arasındaki boşluğun oranıdır. Bunun gibi üst damaktaki ön iki dişin enlerinin toplamının boyların toplamına oranı, 1,618′i vermektedir. Bunlar kuşkusuz standart olarak kabul edilen insan yüzleri için geçerlidir. |
 | Akciğer: Akciğerlerimizin içinde kas ve bağ dokusundan meydana gelen bronşlar ve bunların sıralı olduğu bronş ağacı bulunmaktadır. İşte bu ağacın dallarının uzunlukları arasındaki oran, altın orana eşittir. |
 | DNA: İnsan vücudundaki en küçük elementlerde bile altın orandan bahsedilmektedir. DNA, düşey doğrultuda iç içe açılmış iki ayrı sarmaldan oluşmaktadır ve bu sarmalların uzunluğu 34 angström, genişlikleri 21 angtröm’dür. 21 ve 34 sayıları, Fibonacci sayı dizisinde arka arkaya gelen iki sayıdır ve bunların birbirine oranı altın orandır. |
 | Kar Kristalleri: Kristallerin kollarındaki kısa uzantılarla, uzunlar arasında her zaman altın orana uyan bir ölçü bulunmaktadır. |
 | Geyik Boynuzu: Tıpkı fillerin dişlerindeki sarmal yapılarda olduğu gibi, geyiklerin boynuzlarındaki çıkıntılarda da, 1,618′lik altın oran bulunmaktadır. |
 | Mısır Piramitleri: Milattan önce yapıldığı düşünülen bir yapı olduğu bilinmesine rağmen, altın oranı birebir görebildiğimiz Keops Piramidi’nin taban uzunluğu ile yüksekliğinin birbirine oranı altın oranı vermektedir. |
 | Dişlerde de altın oran vardır. |
 | Ayçiçeği: Tıpkı papatyadaki gibi, çiçeğin merkezinden sağa doğru gidenlerle sola doğru giden taneciklerin oranı altın orana eşittir. Papatyaya benzeyen çiçeklerin neredeyse tamamında bu oran geçerlidir. |
İtalyan matematikçi Leonardo Fibonacci, bir önceki sayı ile toplama esasına dayalı olarak oluşturduğu yandaki dizide yer alan her bir sayının kendisinden önceki sayıya oranlarını incelemiş ve oranın sayı dizisindeki 13. sayıdan ( 144 ) sonra 1,618’ e sabitlendiğini tesbit etmiştir. 1,618 sayısı «Altın Oran» olarak tanımlanır ve Yunan alfabesindeki "Fi" harfi ile sembolize edilir.
«Fibonacci Sayı Dizisi»’ndeki 13. sayı olan 144* sayısından sonra oran 1,618’ e sabitlenmekte ve "Altın Oran" oluşmaktadır. ( * 144 sayısının nümerolojik değeri olan "9" ( 1+4+4 ) sayısının formu, doğadaki varlıklarda görülen spiral forma da işaret eder niteliktedir. )
Nahl 16/18 - Ve (1) in (2) TEUDDU (3) nı'mete (4) allahi (5) la (6) TUHSU (7) ha (8) inne (9) allahe (10) le (11) ğafurun (12) rahım (13)
( Ve eğer Allah' ın nimetlerini SAYARSANIZ, onları SAYAMAZSINIZ. Kesinlikle Allah affedendir merhametlidir. )
( Ve eğer Allah' ın nimetlerini SAYARSANIZ, onları SAYAMAZSINIZ. Kesinlikle Allah affedendir merhametlidir. )
* «Sure» ve «Ayet» numaraları yanyana konduğunda «Altın Oran»’daki ( 1,618 ) rakamlarını da yanyana görmek mümkün olmaktadır.
* Ayette özellille «saymak» fiiline iki kere vurgu yapılmaktadır.
* Ayette toplam 13 kelime bulunmaktadır. ( Fibonacci serisinde Altın Oran 13. sayıdan sonra net olarak ortaya çıkmaktadır. )
* Ayette özellille «saymak» fiiline iki kere vurgu yapılmaktadır.
* Ayette toplam 13 kelime bulunmaktadır. ( Fibonacci serisinde Altın Oran 13. sayıdan sonra net olarak ortaya çıkmaktadır. )
* Ayette Allah’ ın «nimetlerinin» sayılamayacağından bahsedilmektedir.
* Ayette «nimet» kelimesi, son kez olarak «ha» zamiri kullanılarak geçmektedir. Ayetteki «Ha» kelimesinin sıra numarasına göre yapılan hesaplama sonucunda çıkan 1,625 sayısı yaklaşık olarak Altın Oran’ı vermektedir.
Ayrıca iki bölüme ayrılan ayetin ilk bölümü "8", ikinci bölümü "5" kelimeden oluşmaktadır. Ayette toplam "13" kelime bulunmaktadır. Ayetteki toplam kelime adediyle ilk bölümdeki kelime adedinin toplamı "21" olmaktadır. ( 13+8 = 21 ) 21 sayısı "Ruh" kelimesinin Kur'an'daki frekansıdır.
"Altın Oran"ın spiral şeklindeki grafiksel ifadesi, allah'ın yaratışının nümerik sembolü ve ilahi imzası olan "6" sayısına benzemektedir. Allah'ın 6 günde yaratışı konusu Kur'an'da ilk kez A'raf suresinin 54. ayetinde geçmektedir.
7/54 - İnne (1) rabbe (2) kümü (3) allahü (4) ellezi (5) HALEKA (6) es (7) semavati (8) ve (9) el (10) erda (11) fı (12) SİTTETİ (13) eyyamin.... ( Kesinlikle Rab’biniz Allah, gökleri ve yeri ALTI günde YARATTI. ....... )
Ayetteki "Haleka" ( Yarattı ) kelimesinin 6. kelime olması Altın Oran'ın 6 formundaki ( spiral ) grafiksel ifadesi açısından ve "Sitteti" ( Altı ) kelimesinin 13. kelime olması da Fibonacci serisinde Altın Oran olan 1.618 sayısının serideki 13. sayıdan itibaren sabitlenmesi açısından dikkat çekmektedir.
"Altın Oran"'ı sembolize eden harf ise Grek alfabesindeki 21. harf olan "Fi" harfidir. "Fi" harfi, Kur'an'da 1699* kere tekrarlanan "Fi" ( İçinde, Hakkında ) kelimesiyle benzerlik arzetmektedir. Kur'an'da "Fi" kelimesinin ilk kez geçtiği ayette "6" nümerolojisi dikkat çekmektedir. ( * 1699 sayısı da baştaki 1 ve 6 sayıları itibarıyla Altın Oran olan 1.618 sayısını çağrıştırmaktadır. )
2/2 - Zalike (1) el (2) kitabu (3) la (4) raybe (5) Fİ (6) h (7) hüden (8) li (9) el (10) müttekin (11) ( Bu, o HAKKINDA şüphe olmayan, sakınanlar için yönlendirme olan kitaptır. )
Ayetteki "Fi" kelimesi 6. kelimedir. Ayet kodunu oluşturan sayılar ile ayetteki kelime adedini oluşturan sayılar toplandığında yine 6 sayısı elde edilmektedir. ( 2+2+1+1 = "6" )
Fibonacci Sayıları ve Altın Oran Nedir?Şimdi çoğu insan için karmaşık gelen bu 3 maddeyi biraz daha anlaşılır bir dille ifade edip açıklayalım;
1. Altın Oran’ı eski mısırlılar ve yunanlılar bulmuş ve daha çok mimaride kullanmışlardır, basit anlamıyla altın oran; bütünün parçaları arasında olan geometrik ve sayısal bir oran bağlantısıdır.
Bu tanım akıllara şu soruyu getirir; nedir altın oran ve fibonacci arasındaki bağlantı?
Fibonacci dizisindeki ardışık 2 sayının oranı sayılar büyüdükçe Altın Oran’a (1,618) yaklaşır.
Fibonacci Dizisi, her sayının kendisinden bir önceki sayı ile toplanması ile elde edilen sayılar serisidir. Fibonacci Disizinde yer alan rakamların özelliği, Fibonacci Dizisinde yer alan sayıların kendilerinden bir öncekiyle oranlandığında oluşan serinin altın orana yaklaşarak ilerlemesidir.
Fibonacci dizisi 1 rakamı ile başlamak zorunda değildir. Herhangi bir rakam ile başlayabilir.
Örn/ 0-1-1-2-3-5-8-13-bir Fibonacci Dizisidir ancak Fibonacci Dizisi, 4-4-8-12-20-32-52-84 olarak da devam edebilir.
.jpg)
.jpg)
Fibonacci sayı dizisi:
Daha önce 6. yüzyılda Hint matematikçiler tarafından bulunmuş olan bu sayı dizisi Liber Abaci kitabında tavşanların üremesiyle ilgili problemin hesaplanması sonucu Fibonacci tarafından 1202 yılında ortaya konmuştu. Dizinin ilk sayı değeri 0, ikincisi 1 ve her ardışık elemanı da önceki iki elemanın değerinin toplamı alınarak bulunur ve bu halde 0, 1, 1(1+0), 2(1+1), 3(2+1), 5(3+2), 8(5+3), 13(8+5),21(13+8)... şeklinde artar
Daha önce 6. yüzyılda Hintli matematikçiler tarafından bulunmuş olan bu sayı dizisi Liber Abaci kitabında tavşanların üremesiyle ilgili problemin hesaplanması sonucu Fibonacci tarafından 1202 yılında ortaya konmuştu. Dizinin ilk sayı değeri 0, ikincisi 1 ve her ardışık elemanı da önceki iki elemanın değerinin toplamı alınarak bulunur ve bu halde 0, 1, 1(1+0), 2(1+1), 3(2+1), 5(3+2), 8(5+3), 13(8+5),21(13+8)... şeklinde artar.
Fibonacci Dizisine neden Fibonacci Dizisi Denilir ?
Fibonacci Dizisi Leonardo Fibonacci tarafından bulunmuştur. İtalya’da doğmuş olan Leonardo Fibonacci bir problemi araştırırken bu sayıları keşfeder ve kendi adını vermeye karar verir.
Fibonacci Dizisi Neden Bu Kadar Önemlidir ?
Fibonacci Dizisi Nedir başlığında da bahsettiğimiz gibi, dizideki sayıların kendinden önceki sayıya bölünmesiyle altın orana yaklaşılması ve altın oranın da hayatımızdaki objelerin içinde yer alması bu sayıları önemli ve gizemli kılmıştır. Fibonacci Dizisinde yer alan altın oran, eski Mısırlılar bulmuşlardır. Yunanlılar da, Mısırlılar gibi bu sayıyı mimaride kullanmışlardır. Altın oranı basitçe anlatmak gerekirse,
Bütünü oluşturan parçalar arasındaki geometrik orandır.
İnsan yüzünde de birçok altın oran vardır. Ama bu oranlandırma, bilim adamları ve sanatkarların beraberce kabul ettikleri "ideal bir insan yüzü" için geçerlidir. Örneğin üst çenedeki ön iki dişin enlerinin toplamının boylarına oranı altın oranı verir. İlk dişin genişliğinin merkezden ikinci dişe oranı da altın orana dayanır. Bunlar bir dişçinin dikkate alabileceği en ideal oranlardır. Bunların dışında insan yüzünde yer alan diğer bazı altın oranlar şöyledir:
- Yüzün boyu / Yüzün genişliği,
- Dudak- kaşların birleşim yeri arası / Burun boyu,
- Yüzün boyu / Çene ucu-kaşların birleşim yeri arası,
- Ağız boyu / Burun genişliği,
- Burun genişliği / Burun delikleri arası,
- Göz bebekleri arası / Kaşlar arası.
Mesela Leonardo da Vinci, Fibonacci'nin altın oranını ünlü Mona Lisa tablosunda kullanmıştır. Bu tablonun boyunun enine oranı altın orandır. Aynı oranlar Mona Lisa'nın yüzünün etrafına çizilen dikdörtgende de vardır. Bu dikdörtgeni göz hizasında çizilen çizgiyle ikiye ayırırsanız yine altın oranı elde edersiniz.
Ayrıca Leonardo da Vinci, 1509'da Luca Pacioli'nin yayımladığı İlahi Oran adlı bir çalışmasına resimler vermiştir. Bu kitapta Leonardo Leonardo da Vinci tarafından yapılmış Five Platonic Solids (Beş Platonik Cisim) adlı resimler bulunmaktadır. Bunlar, bir küp, bir Tetrahedron, bir Dodekahedron, bir Oktahedron ve bir Ikosahedronun resimleridir. Altın Oran'ın Latince karşılığını ilk kullanan muhtemelen Leonardo da Vinci 'dir. Rönesans sanatçıları Altın Oran'ı tablolarında ve heykellerinde denge ve güzelliği elde etmek amacıyla sıklıkla kullanmışlardır. Örneğin Leonardo da Vinci, Son Yemek adlı tablosunda, İsa'nın ve havarilerin oturduğu masanın boyutlarından, arkadaki duvar ve pencerelere kadar Altın Oran'ı uygulamıştır.
Günlük hayatımızdan örnekler ile Fibonacci Dizisini açıklamaya çalışırsak,
İşaret parmağımızın bir önceki boğum ile oranı altın oranı vermektedir.
Fibonacci Dizisi ile ulaşabildiğimiz altın oran insan yüzündeki duyu organlarının oranlamasıyla da ortaya çıkmaktadır. Örneğin, kulaklarımızın, burnumuzun altından çenemize kadar olan alan altın oranı içermektedir.
Mısır Piramitlerinde de tabanının yüksekliğine oranı altın oranı vermektedir.
İnsan vücudundaki altın oranları keşfetmek için çeşitli ölçümler ve hesaplamalar yapabiliriz.
Öğrencilerimizle birlikte Fibonacci veya Altın Oran temalı tişörtler tasarlayabiliriz.
Gelelim Dünya nın Altın Oranı na :
Fi sabiti- 1,618, matematikteki üstün tasarım sayısı. Kalp atışlarımızda, DNA sarmallarının en ve boy oranında, kainatın dodecehadron adı verilen özel tasarımında, bitkileirn filotaksi denen yaprak dizilim kurallarında, kar tanesi kristallerinde, pek çok galaksinin spiral yapısında ve sayısız yerde Yaratıcı hep aynı muhteşem sayıyı kullanmıştı. Altın oran sayısı yani 1,618…
Pek çok ünlü mimari yapıda olduğu gibi Mısır Piramiterlerinin tasarımında dahi bu oranın kullanıldığı görülmektedir. Ünlü astronom Kepler, bu sayı için büyük bir hazine ifadesini kullanmıştı. Yüzlerce yıldır pek çok ünlü ressam, mühendis ve mimar Leonardo da Vinci gibi neredeyse tüm eserlerinde bu oranı kullanıyorlardı.
Estetik uzmanı Dr Steven Markout 25 yıl süren araştırmasında DNAmıza dahi işlenmiş bu orana göre yaratılmış insan yüzleri ve bedenlerini istisnasız tüm insanların güzel bulduğunu yaptığı büyük bir deneyle ispatladı. Bir şekli tanımlayan temel ölçülerin birbirine oranının 1,618 i vermesi onu Altın Oran’a yani kusursuz tasarıma uygun hale getiriyordu.
Peki ya dünyamızın Altın Oran Noktası… nerededir?
Mekke şehrinin kuzey kutup noktasına olan uzaklığı ile güney kutup noktasına olan uzaklığının oranı tam olarak 1,618 yani altın orandır. Ayrıca Mekke şehrinin Güney kutup noktasına olan uzaklığı ile iki kutup arasındaki uzaklığın birbirine oranı yine 1,618 dir.
Mucize bununla bitmez; tüm insanlığın ortak yer belirleme dili haline gelmiş enlem boylam haritasına göre de Dünyanın Altın Oran noktası Mekke şehrindedir.
Mekke’den günleri değiştiği ve gün dönümü çizgisi olarak belirtilen sınıra olan doğu uzaklığı ile batı uzaklığının birbirine oranı da yine 1,618 dir. Ayrıca Mekke’nin gündönümü çizgisine batı yönlü uzaklığının, dünyanın o enlemdeki çevre uzunluğuna oranı da şekilde görüldüğü gibi yine şaşırtıcı şekilde Altın oran yani 1,618 sayısını verir. Tüm harita sistemlerindeki bir kaç km olan ufak farklara rağmen Altın Oran noktası Mekke şehrinden asla dışarı çıkmaz ve Kabe’yi içine alan Kutsal Bölge dairesinde kalır.
Evinizde Google Earth programı’nın cetvel özelliğini kullanarak dünyadaki herhangi iki nokta arasındaki uzaklığı oldukça hassas şekilde kolayca keşfedebilir, Dilerseniz enlem ve boylam koordinatları yoluyla hesaplayarak yada basit bir hesap makinesi ile verilen oranların doğruluğunu evinizde dahi test edebilirsiniz. Görüntülerde önce Mekke şehrine sonra Kuzey Kutup noktasına başlangıç ve bitiş noktalarını nasıl yerleştirildiğini görüyorsunuz. Pozitif enlem ve boylam değerleri ile deniz yerine Karaya düşme açısından dünyanın tek altın Oran noktası Mekke şehri olabilmektedir.
Phi matrix programı ise tabloların ve resimlerin altın oran noktasını göstremeye yarayan bir Amerikan programıdır. Dünya Enlem boylam haritasını derinliği hiç bitmeyen canlı bir tablo gibi düşünür ve bu programla açarsak Dünyanın Altın Oran noktasının Mekke şehri olarak belirlendiğini görürüz.
Mekke ayetinde Altın Oran Mucizesi
Kuran ı Kerimde Mekke kelimesinin geçtiği ve orada tüm insanlığa iman verecek açık delillerin varlığından bahseden tek bir ayet vardır. Ali İmran Suresi 96. ayetinde Mekke şehri ile Altın oran arasındaki bağıntı Yüce Yaratıcımız tarafından açıkca nakşedilmiştir. Bu ayetin tüm harf sayısı 47 dir. harf sayılarının altın oranını aldığımızda Mekke kelimesinin işaret edildiğini görürüz. 47 / 1,618 = 29,0 . Ayet başından Mekke kelimesine kadar tam 29 harf vardır. Aynı dünya haritasındaki gibi. Eğer bir harf fazla yada eksik olsa idi bu oran asla oluşmayacaktı. Hiç bir zorlama olmadan dünya üzerinde yaptığımız aynı işlemi yaptık ve harf sayılarının mekke ve altın oranı işaret eden muhteşem uyumuna şahit olduk.
Tüm bu işaretler göstermektedir ki; dünyayı ve matematiği yaratan tasvir edilmesi imkansız muhteşem güç yani Tanrı ile Kabe’nin ve Kutsal Bölgenin yer belirleyicisi ile Kuran’ın yaratıcısı aynı ve tek Tanrıdır. O bu mucizelerle geleceği ve insanların ortak dillerini önceden bilerek onlara işaretler verdiğini tüm insanlığa hatırlatmaktadır.
Altın Oran, Mekke, Kabe ve Kuran arasındaki bağıntılarla ilgili keşifler her geçen gün bir yenisi eklenmektedir. Şekilde Leonardo pergeli olarak adlandırılan Altın oran pergeli ile yapılmış ölçümlerde Mekke şehrinin Arabistanın altın oran bölgesinde, Kabeninde Mekke şehrinin altın oran bölgesinde yer aldığını görüyoruz. Tüm bunların tesadüfen olabilmesi olasık hesaplarına göre imkansızdır.
FİBONACCİ DİZİSİNİN FİNANS SEKTÖRÜNDE KULLANIMI
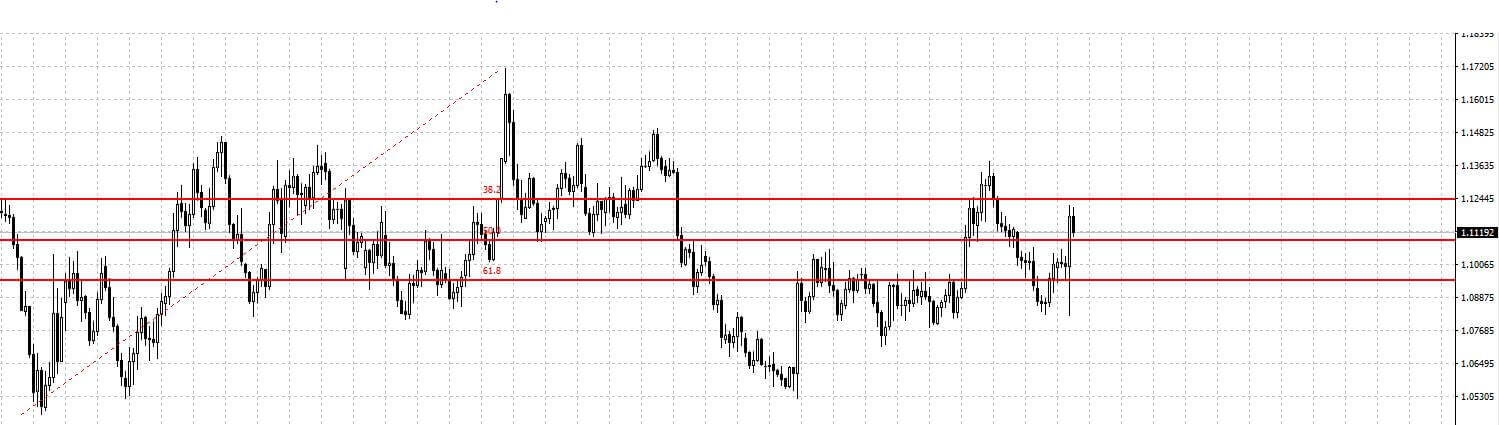
FİBONACCİ DÜZELTME SEVİYELERİ ( RETRACEMENT )
Fibonacci Dizisi finans sektöründe finansal varlıkların alacakları değeri tahminlemede kullanılır. Teknik analiz uygulamalarında kullanılan Fibonacci Dizisi ile ulaşabileceğimiz altn orandır. Genel olarak kullanılan oranlar, 1.618 ve 1.232’dir.
ÖRN/ Baz aldığımız zaman aralığında en düşük fiyatı 1,0520, en yüksek fiyatı ise 1,1376 seviyesini görmüş olan bir pariteyi ele alalım.
Yüksek fiyat ile düşük fiyatı birbirinden çıkarttığımızda, 1,1376 – 1,0520 = 0,0856 olacaktır. Bu değeri yukarıdaki 1.272 ile çarptığımızda, 0,0856 * 0.232 = 0,0198 olacaktır. Bu değeri yüksek fiyat olan 1,1376’ ya eklediğimizde, 1,1578 olacaktır. Bu ortaya çıkan değer paritenin yükselmesini beklediğimiz trendi ortaya koyar.
.png)
Bu örnekten de anlaşılabileceği gibi, finans sektöründe bir paritenin hareketinin kesintisiz oluşması beklenemez. Fibonacci Dizisi bu trendi belirlememizde yardımcı olabilecek analizler sunmaktadır.
Fibonacci Dizisi’nin finans sektöründe bir diğer kullanımı da Fibonacci Zaman Aralıkları’dır.
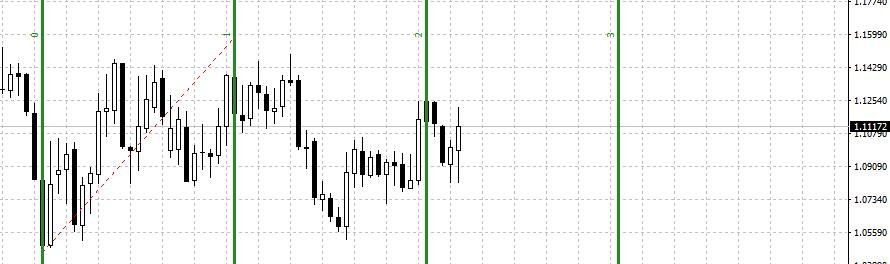
FİBONACCİ ZAMAN ARALIKLARI NEDİR ?
Yukarıda bahsettiğimiz analiz yöntemlerindeki tek değişken fiyat değildir. Zaman değişkenin de kapsamlı olarak incelenmesi gereklidir. Bu bağlamda Fibonacci Dizileri fiyat değişimlerinde kullanıldığı gibi zaman aralıklarında da kullanılabilir. Zaman aralıkları belirlenirken Fibonacci Dizisi’ndeki rakamlar gün olarak baz alınır yani, 1-1-2-3-5-8-13-21-34 şeklinde trend gün aralıklarına bölünür. Bu analiz dalgalanmaların süresini tespit etmekte kullanılmaktadır.
FİBONACCİ YAYLARI NEDİR ?
Fibonacci Yayları paritenin izlediği trendin taban seviyesinden tavan seviyesine çizilen referans çizgisi ile oluşturulur. Bu çizginin %81.8, %50 ve %38.2 seviyelerine çizilen yaylara Fibonacci Yayları denir.
Fibonacci Yayları analiz yönteminde fiyat yaya yukarıdan yaklaşıyorsa destek, aşağıdan yaklaşıyorsa direnç olarak yorumlanır.
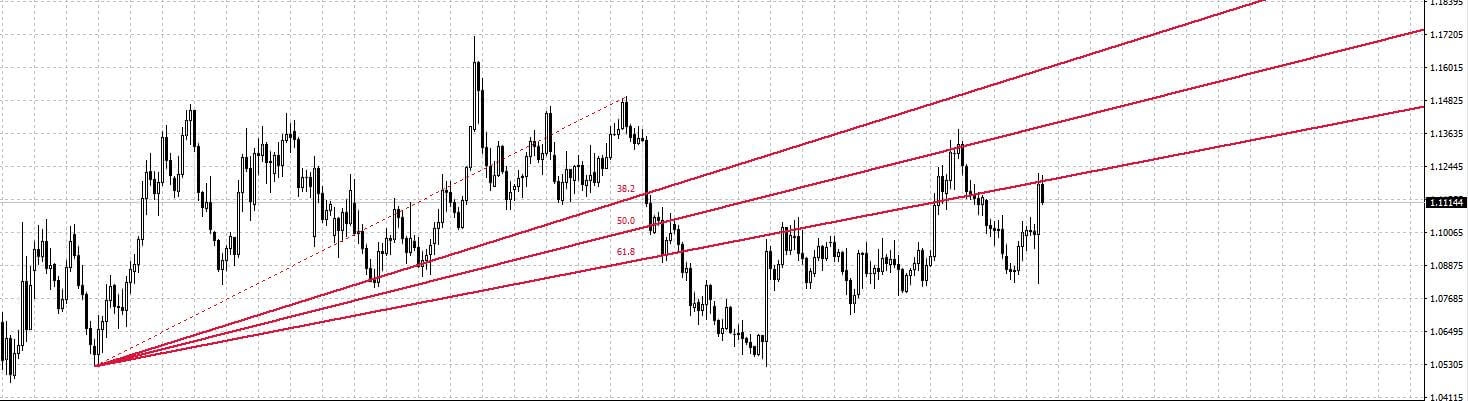
FİBONACCİ FANLARI NEDİR ?
Fibonacci Dizisi’nin finansal analizlerdeki diğer kullanım alanı da, Fibonacci Fan Çizgileridir.
Diğer Fibonacci Analizlerinde de bahsettiğimiz gibi Fibonacci Fanlarında da taban ve tavan noktalarına klavuz çizgi çizilir. Bu klavuz çizgi ana trendin değil ara trendin tavan noktasına çizilmelidir.
Fibonacci Fan Analizi doğruluğu kesinleşmiş bir analiz yöntemi değildir. Bunun sebebi, volatil piyasalarda ya da dönemlerde yanılma payının artmasıdır. Bu sebeple daha istikrarlı stabil piyasalarda uygulanması önerilir.
Daha Fazla Radyo için 
Daha Fazla Televizyon için 
Hiç yorum yok:
Yorum Gönder